计算考虑

最重要的一个技术计算中存在的问题的解决方案是系统的线性方程组。

在矩阵表示法,一般问题采取以下形式:两个矩阵一个和b是否存在一个独特的矩阵x,所以一个x=b或x一个=b吗?

考虑一个1×1的例子是很有意义的。例如,方程

有一个独特的解决方案吗?

当然,答案是肯定的。方程有唯一解x= 3。解决方案是容易获得的部门:

解决方案是不通常通过计算得到的逆7,这是7¹= 0.142857……,then multiplying 7¹由21。这将是更多的工作,如果7¹有限数量的数字,表示不准确。类似的考虑也适用于集多个未知的线性方程组;MATLAB^®解决这些方程计算矩阵的逆。

尽管它不是标准的数学符号,MATLAB使用部门术语熟悉标量案例来描述解决方案的联立方程组。这两个部门符号,削减、/、反斜杠、\对应两个MATLAB函数mrdivide和mldivide。这些操作符用于未知矩阵的两种情况出现在左边或者右边的系数矩阵:

认为“分裂”方程两边斧头=b或xA=b通过一个。系数矩阵一个总是在“分母”。

维兼容性条件x = A \ b需要两个矩阵一个和b有相同数量的行。解决方案x然后有相同数量的列b及其行维度等于列维度一个。为x = b / A,行和列的角色互换。

在实践中,线性方程的形式斧头=b比形式更频繁地发生xA=b。因此,使用反斜杠比削减更频繁。本节的其余部分集中在反斜杠符;相应的削减操作符的属性可以推断从身份:

(b / A) = (“\ b”)。

系数矩阵一个不需要广场。如果一个有大小米——- - - - - -n,然后有三种情况:

通解

线性方程组的通解斧头=b描述所有可能的解决方案。万博 尤文图斯你可以找到的通解:

你可以写任何解决方案斧头=b作为特定解决方案的总和斧头=b从步骤2,加上从步骤1基向量的线性组合。

本节的其余部分描述了如何利用MATLAB来找到一个特定的解决方案斧头=b,如步骤2。

广场系统

最常见的情况就是一个方形系数矩阵一个和一个右边列向量b。

一个=帕斯卡(3);u = [3;1;4);x = \ u x = -12 5

b =魔法(3);X = A \ b X = 19 13 6 0 6 3 1 -17 4

P = pinv b (A) *

一个= [1 3 7 1 4 4 1 10 18]

排名(A) ans = 2

pinv (A) * b ans = 0.3850 -0.1103 0.7066

* pinv () * b ans = 5.0000 2.0000 12.0000

* pinv () * b ans = -1.0000 4.0000 2.0000

rref ([b]) ans 2.2857 = 1.0000 0 0 0 0 0 0 0 1.0000 1.0000 - 1.5714

超定的系统

这个例子展示了如何超定的系统中经常遇到各种各样的曲线拟合实验数据。

一个量y在几个不同的时间值来衡量吗t产生以下的观察。您可以输入数据,并把它在一个表中使用以下语句。

t = [0。3。8 1.1 1.6 2.3] ';y = [。82 .72点.60 55 .50]”;表(t, B = y)

B =6×2表t y ___ ____ 0 0.82 0.3 0.72 0.8 0.63 1.1 0.6 1.6 0.55 2.3 0.5

尝试建模数据与一个指数衰减函数

$y(t)=c_1+c_2{e}^{-\; -\; -\; -\; -\; -t}$。

前面的方程表示,向量y应该是用两个向量的线性组合近似。一个是一个常数向量包含所有的,另一个是向量和组件exp (- t)。未知系数, $$c_1$$和 $$c_2$$,可以通过最小二乘匹配计算,减少偏差的平方之和的数据模型。有六个方程两个未知数,由6-by-2表示矩阵。

E =[(大小(t)) exp (- t))

E =6×21.0000 1.0000 1.0000 0.7408 1.0000 0.4493 1.0000 0.3329 1.0000 0.2019 1.0000 0.1003

使用反斜杠运算符的最小二乘解。

c = E \ y

c =2×10.4760 - 0.3413

换句话说,最小二乘适合数据

以下语句用于评估模型在定期间隔的增量t,然后绘制结果与原始数据:

T = (0:0.1:2.5)”;Y =[(大小(T)) exp (- T)] * c;情节(T Y“- - -”、t、y,“o”)

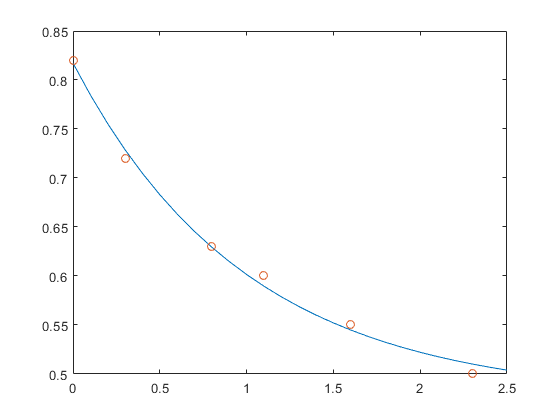
E * c并不完全等于什么y,但是差异很可能低于测量原始数据中的错误。

一个矩形矩阵一个是等级不足,如果没有线性独立的列。如果一个等级不足,那么最小二乘解AX = B并不是唯一的。一个\ B问题一个警告如果一个等级不足,产生一个最小二乘解。您可以使用lsqminnorm找到解决方案X在所有解决方案的最低标准。万博 尤文图斯

欠定的系统

这个例子显示了如何解决欠定的系统并不是唯一的。欠定的线性系统涉及比方程未知数。在MATLAB矩阵左部操作发现一个基本的最小二乘解,最多米为一个非零组件米——- - - - - -n系数矩阵。

这是一个小,随便举个例子:

R = [6 7 8 3;3 4 5 1]rng (0);b =兰迪(2,1)

R = 6 7 8 3 3 5 4 1 b = 7 8

线性系统Rp = b涉及到两个方程在四个未知数。由于系数矩阵包含小整数,它是适当的使用格式命令显示解决方案在rational格式。特定的解

格式老鼠p = R \ b

p = 0 17/7 0 -29/7

一个非零组件(2页)因为R (: 2)的列R与最大的常态。另一个非零组件(4页)因为R (: 4)后占主导地位R (: 2)就被消除了。

完整的通解欠定的系统可以通过添加特征p对一个任意零空间向量的线性组合,可以发现使用零函数与一个选项要求理性的基础上。

Z = null (R,“r”)

Z = 1/2 -7/6 1/2 1/2 1 0 0 1

它可以证实R * Z是零,剩余R * x - b任何向量小吗x,在那里

x = p + Z *

自列Z零空间向量,是产品吗Z *问是一个向量的线性组合:

为了说明这一点,任意选择问和构建x。

q = [2;1);x = p + Z *;

计算剩余的规范。

格式短规范(R * x - b)

ans = 2.6645 e15汽油

当无限多的解决方案是可用的,最低标准的解决万博 尤文图斯方案是特别感兴趣的。您可以使用lsqminnorm计算minimum-norm最小二乘解。这个解决方案的最小值常模(p)。

p = lsqminnorm (R, b)

p = -207/137 365/137 79/137 -424/137

解决几个右手边

一些问题都集中在解决线性系统有相同的系数矩阵一个,但是不同的右手边b。当不同的值b可与此同时,你可以构建b作为一个包含多个列的矩阵,解决所有的系统方程同时使用一个反斜杠命令:X = A \ [b1 b2 b3…]。

然而,有时不同的值b不是所有可用的同时,这意味着你需要解决几个系统的连续方程。当你解决这些系统的方程使用斜杠(/)或反斜杠(\),操作者因式分解的系数矩阵一个并使用这个矩阵分解计算的解决方案。然而,每个随后的时候用一个不同的解决类似的方程组b,操作员计算相同的分解一个,这是一个冗余计算。

此问题的解决方案是预先执行分解一个的因素,然后重用来解决不同的值的b。然而在实践中,预先执行分解以这种方式是很困难的,因为你需要知道哪些分解计算(LU,低密度脂蛋白,柯列斯基,等等),以及如何用因素来解决这个问题。例如,LU分解需要解决两个线性系统来解决原系统Ax = b:

陆[L U] =(一个);x = U \ (L \ b);

相反,推荐的方法求解线性系统和几个连续的右手边是使用分解对象。这些对象允许您利用预计算的性能优势矩阵分解,但他们不需要如何使用矩阵的知识因素。你可以替换以前的LU分解:

dA =分解(,“陆”);x = dA \ b;

如果你不确定使用哪个分解,分解(一)选择正确的类型属性的基础上一个,类似于什么反斜杠。

这是一个简单的测试可能的这种方法的性能优势。测试解决相同的稀疏线性系统使用两个反斜杠(\)和100倍分解。

n = 1 e3;一个= sprand (n, n, 0.2) + speye (n);b = 1 (n, 1);%反斜杠的解决方案抽搐为k = 1:10 0 x = \ b;结束toc

运行时间是9.006156秒。

%分解方案抽搐dA =分解(A);为k = 1:10 0 x = dA \ b;结束toc

运行时间是0.374347秒。

对于这个问题,分解解决方案是比单独使用反斜杠快得多,但语法仍然是简单的。

迭代的方法

如果系数矩阵一个是大而稀疏分解方法一般不高效。迭代的方法产生一系列的近似解。万博 尤文图斯MATLAB提供几种迭代方法处理大型、稀疏矩阵输入。

多线程计算

MATLAB支万博1manbetx持多线程计算的线性代数和element-wise数值函数。这些函数自动执行多个线程。函数或表达式执行得更快在多个cpu,大量的条件必须是真实的:

发票,lscov,linsolve,mldivide在大型双精度数组显示显著增加的速度(10000个元素的顺序或更多)启用多线程时。