微分方程

这个例子展示了如何使用MATLAB®制定和解决不同类型的微分方程。MATLAB提供了几个数值算法来解决各种各样的微分方程:

初始值的问题
边值问题
延迟微分方程
偏微分方程

初值问题

vanderpoldemo是一个函数,定义了范德波尔方程

$\frac{d^{2} y}{d t^{2}} - - - - - - μ (1 - - - - - - y^{2}) \frac{d y}{d t} + y = 0 。$

类型vanderpoldemo

函数dydt = vanderpoldemo (t, y,μ)% vanderpoldemo定义ODEDEMO范德波尔方程。% 1984 - 2014版权MathWorks公司dydt = [y (2);μ* (1 y (1) ^ 2) * y (2) - y (1)];

方程被编写为一个系统的两个一阶常微分方程(常微分方程)。这些方程是评估不同的参数值 $μ$ 。更快的集成,你应该选择一个适当的基于价值的解决者 $μ$ 。

为 $μ = 1$ ,任何的MATLAB解决歌唱能有效地解决范德波尔方程。的数值解算器就是这样一个例子。方程是解决的领域 $(0, 20.]$ 与初始条件 $y (0) = 2$ 和 $\frac{dy}{dt} |_{t = 0} = 0$ 。

tspan = 20 [0];y0 = [2;0);μ= 1;颂歌= @ (t, y) vanderpoldemo (t yμ);[t、y] =数值(tspan颂歌,y0);%策划解决方案情节(t, y(: 1))包含(“t”)ylabel (“解决方案y”)标题(“范德波尔方程\μ= 1”)

图包含一个坐标轴对象。坐标轴对象标题范德波尔方程、μ空白=空白1,包含t y ylabel解决方案包含一个类型的对象。

对于更大的大小的 $μ$ ,问题就僵硬的。这个标签问题,抵制试图与普通技术评估。相反,需要特殊的数值方法快速集成。的ode15s,ode23s,ode23t,ode23tb函数可以有效地解决僵硬的问题。

这个解决方案的范德波尔方程 $μ = 1000年$ 使用ode15s相同的初始条件。你需要伸展时间跨度极大 $(0, 3000年]$ 能够看到的周期性运动解决方案。

tspan = [0, 3000);y0 = [2;0);μ= 1000;颂歌= @ (t, y) vanderpoldemo (t yμ);[t、y] = ode15s (tspan颂歌,y0);情节(t y(: 1)标题(“范德波尔方程\μ= 1000”轴([0 3000 3 3])包含(“t”)ylabel (“解决方案y”)

图包含一个坐标轴对象。坐标轴对象标题范德波尔方程、μ空白= 1000,包含t y ylabel解决方案包含一个类型的对象。

边值问题

bvp4c和bvp5c解常微分方程的边值问题。

函数的例子twoode有一个微分方程写成两个一阶常微分方程的系统。微分方程是

$\frac{d^{2} y}{d t^{2}} + | y | = 0 。$

类型twoode

=函数就要twoode (x, y) % twoode评估TWOBVP的微分方程。% %参见TWOBC TWOBVP。%劳伦斯·f·Shampine和Jacek Kierzenka % MathWorks版权1984 - 2014,公司就要= [y (2);abs (y (1)));

这个函数twobc有问题的边界条件: $y (0) = 0$ 和 $y (4) = - - - - - - 2$ 。

类型twobc

函数res = twobc(是的,yb) % twobc评估剩余TWOBVP的边界条件。% %参见TWOODE TWOBVP。%劳伦斯·f·Shampine和Jacek Kierzenka % 1984 - 2014版权MathWorks, inc . res =[丫(1);yb (1) + 2];

之前调用bvp4c,你必须提供一个猜你想要的解决方案表示在一个网格。然后解决适应网格的改进解决方案。

的bvpinit功能组装初始猜的形式可以通过解算器bvp4c。的网[0 1 2 3 4)和不断的猜测 $y (x) = 1$ 和 $y ' (x) = 0$ 时,调用bvpinit是:

solinit = bvpinit ([0 1 2 3 4], [1;0]);

这个最初的猜测,你可以解决的问题bvp4c。评估返回的解决方案bvp4c在一些点使用德瓦尔,然后情节产生的值。

索尔= bvp4c (@twoode @twobc solinit);xint = linspace (0、4、50);yint =德瓦尔(溶胶,xint);情节(xint yint (1:));包含(“x”)ylabel (“解决方案y”)举行在

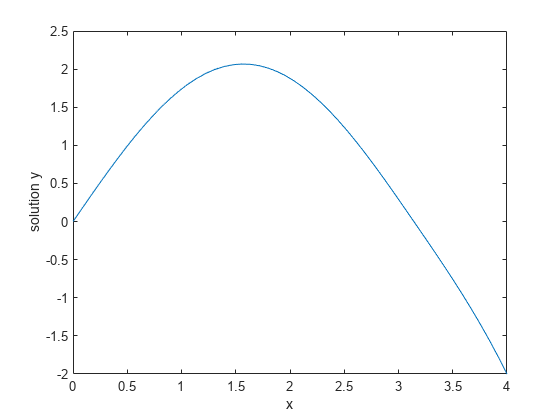
图包含一个坐标轴对象。坐标轴对象包含x, y ylabel解决方案包含一个类型的对象。

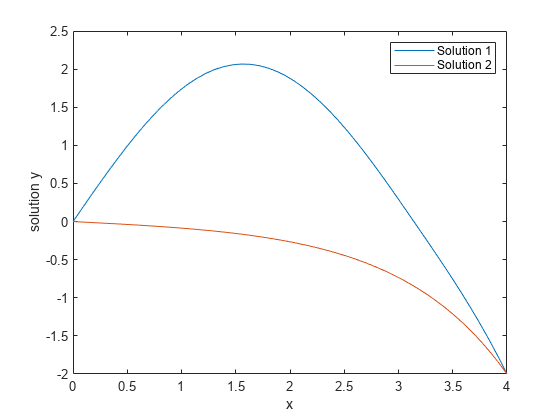
这个特殊的边值问题有两种解决方案。万博尤文图斯你可以获得其他解决方案通过改变最初的猜测 $y (x) = - - - - - - 1$ 和 $y ' (x) = 0$ 。

solinit = bvpinit ([0 1 2 3 4], [1;0]);索尔= bvp4c (@twoode @twobc solinit);xint = linspace (0、4、50);yint =德瓦尔(溶胶,xint);情节(xint yint (1:));传奇(“方案1”,的解决方案2)举行从

图包含一个坐标轴对象。坐标轴对象包含x, y ylabel解决方案包含2线类型的对象。这些对象代表解决方案1,方案2。

延迟微分方程

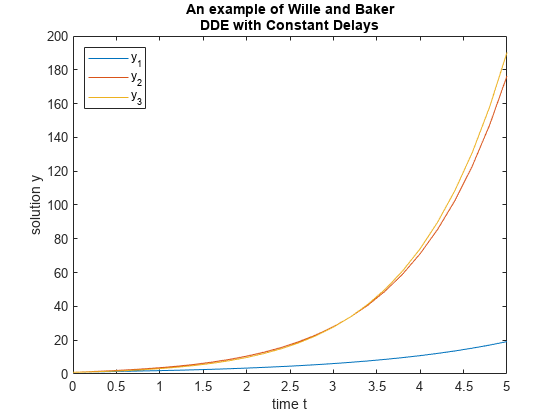
dde23,ddesd,ddensd解时滞微分方程与各种延误。的例子ddex1,ddex2,ddex3,ddex4,ddex5形成一个迷你教程使用这些解决方案。

的ddex1示例显示了如何解决微分方程组

$\begin{array}{l} y_{1}^{”} (t) = y_{1} (t - - - - - - 1) \\ y_{2}^{”} (t) = y_{1} (t - - - - - - 1) + y_{2} (t - - - - - - 0 。 2) \\ y_{3}^{”} (t) = y_{2} (t) 。 \end{array}$

这些方程可以用匿名函数

ddex1fun = @ (t, y, Z) [Z (1,1);(1)+ Z (2, 2);y (2)];

(历史的问题 $t \leq 0$ )是不变的:

$\begin{array}{l} y_{1} (t) = 1 \\ y_{2} (t) = 1 \\ y_{3} (t) = 1 。 \end{array}$

你可以代表的历史作为一个向量的。

ddex1hist = 1 (3,1);

一个双元素向量表示方程组的延迟。

滞后= 0.2 [1];

传递函数,延迟,解决历史和间隔的集成 $(0, 5]$ 解算器作为输入。解算器产生一个连续的集成解决方案在整个区间适合策划。

索尔= dde23 (ddex1fun滞后、ddex1hist [0 5);情节(sol.x sol.y);标题({威利和贝克的一个例子,DDE常延迟的});包含(“t”);ylabel (“解决方案y”);传奇(“y_1”,“y_2”,“y_3”,“位置”,“西北”);

图包含一个坐标轴对象。坐标轴对象与标题的一个例子威利和贝克DDE不断延迟,包含时间t, ylabel解y包含3线类型的对象。这些对象代表y_1, y_2 y_3。

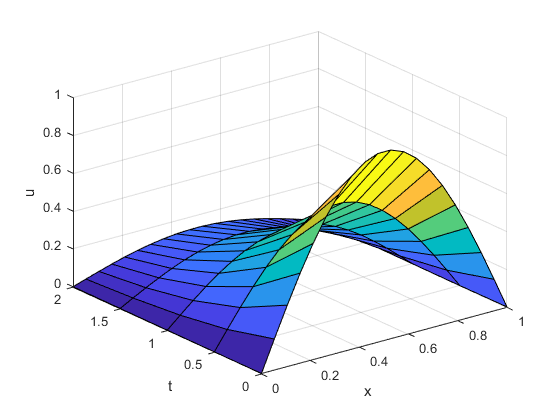
偏微分方程

pdepe解决了偏微分方程在一个空间变量和时间。的例子pdex1,pdex2,pdex3,pdex4,pdex5形成一个迷你教程中使用pdepe。

这个例子使用功能问题pdex1pde,pdex1ic,pdex1bc。

pdex1pde定义了微分方程

$π^{2} \frac{\partial u}{\partial t} = \frac{\partial}{\partial x} (\frac{\partial u}{\partial x}) 。$

类型pdex1pde

函数[c、f、s] = pdex1pde (x, t, u, DuDx) % pdex1pde评估PDEX1问题的微分方程组件。% %参见PDEPE PDEX1。%劳伦斯·f·Shampine和Jacek Kierzenka % 1984 - 2014版权MathWorks, inc . c =π^ 2;f = DuDx;s = 0;

pdex1ic设置初始条件

$u (x, 0) = 罪 π x 。$

类型pdex1ic

函数情况= pdex1ic (x) % pdex1ic评估PDEX1编码问题的初始条件。% %参见PDEPE PDEX1。%劳伦斯·f·Shampine和Jacek Kierzenka % MathWorks版权1984 - 2014,公司情况=罪(π* x);

pdex1bc设置边界条件

$u (0, t) = 0,$

$π e^{- - - - - - t} + \frac{\partial}{\partial x} u (1, t) = 0 。$

类型pdex1bc

函数(pl ql,公关,qr] = pdex1bc (xl, ul, xr, ur, t) % pdex1bc评估PDEX1编码问题的边界条件。% %参见PDEPE PDEX1。%劳伦斯·f·Shampine和Jacek Kierzenka % 1984 - 2014版权MathWorks, inc . pl = ul;ql = 0;公关=π* exp (- t);qr = 1;

pdepe需要的空间离散化x和一个向量的时间t(你想要一个解决方案的快照)。解决这个问题使用20节点和请求的网格解决方案5的值t。提取和情节的第一个组件的解决方案。

x = linspace (0, 1, 20);t = 0.5 [0 1 1.5 - 2);索尔= pdepe (0 @pdex1pde @pdex1ic @pdex1bc x, t);u1 =索尔(:,:1);冲浪(x, t, u1);包含(“x”);ylabel (“t”);zlabel (“u”);

图包含一个坐标轴对象。对象包含x轴,ylabel t包含一个类型的对象的表面。

另请参阅

数值|bvp4c|pdepe